Adjoints for shape optimization: Inkjet microchannels

I have recently given a talk about shape optimization using adjoints (work done by me and Prof. Matthew Juniper). We applied the adjoint approach and finite elements method to improve the performance of inkjet drop-on-demand printers. We proposed a way to increase the printing speed by controlling the acoustic properties of the flow.

What is inkjet printing?

Inkjet drop-on-demand printing is modern printing technology with precise control of fluid deposition and a wide range of possible printing materials. Inkjet printers are extensively used in industry to print pictures, patterns and labels onto various substrates. Increasingly they are used for 3D printing and advanced manufacturing.

Inkjet drop-on-demand printers are known for high printing resolution and capability of jetting up to 100 000 droplets per second. This allows printing lines to run at the speed of 50 meters per minute.

This is an example of a printhead, which is the core part of every inkjet printer. It contains thousand ink-filled parallel narrow channels.

Printhead’s microchannel: overview

A generic geometry of a printhead’s microchannels is a U-shaped channel, connected to ink-supply manifolds. Each microchannel has a piezo-electric actuator on one side and a 20 micron nozzle on the opposite side.

Overall, the physics of the flow is quite complex. It is an unsteady compressible flow with advection, viscous and thermal effects. The dynamics of the nozzle meniscus is a free surface problem coupled to the flow motion inside the channel.

Generally, we can distinguish two main sources of fluid motion inside the microchannels.

The first source is a continuous slow through flow. In inkjet printers, it is crucial that every nozzle functions identically and that all drops are the same. A nozzle can stop working if it is blocked by air bubbles and solid impurities. It then leaves a straight unprinted line on the substrate. For this reason, special pumps maintain the pressure drop so ink is flushed continually through the channels.

The second source is the piezoelement, which oscillates and creates acoustic waves. Both the through flow and the flow, generated by the piezoelectric actuator are low Reynolds and low Mach number flows.

Printing cycle: ejection and reverberation stages

When a drop is demanded, an electric signal is applied to the actuator. A positive signal deforms the channel boundary by several hundred nanometers, and pressure waves appear inside the channel. When they reach the nozzle meniscus, the free surface deforms. This forces an ink droplet out of the nozzle. After the main pulse ends, the actuator moves back, and acoustic oscillations reverberate within the channel, decaying through viscous and thermal dissipation.

If the acoustic reverberations from the previous droplet have not died away sufficiently when the next droplet is demanded, the pressure waves overlap, affecting the next droplet. Image sharp edges become fuzzy. The time required for the residual oscillations to die away limits the printing rate.

In our study, we aim to shorten this last stage. That this can be done by increasing the decay rate of the acoustic oscillations.

Shape optimization: general formulation

Since we have two independent sources of low Mach number motion, we can formally separate the fully compressible Navier-Stokes equations into two parts. The first part is the steady flow with no oscillations, governed by the incompressible Navier-Stokes equations. This represents the through flow which flushes the ink through the channel. The second part is the acoustic oscillating flow with no steady flow, governed by the viscothermal acoustic equations, and represents the acoustic waves propagation.

Now we have two smaller problems, and we aim to understand whether it is possible to modify the generic geometry such that

• the steady flow pressure drop stays the same, because we don’t want to use more powerful pumps, and
• damp the residual acoustic reverberations which remain inside the channel after the pulse ends.

We define two objective functions:

1. The steady flow viscous dissipation, which is a proxy for the pressure drop and an easier numerical problem,

   \[\begin{equation} \mathcal{R} = \int_\Omega \nu \left( \nabla \mathbf{u} \right)^2 \end{equation}.\]

2. The oscillating flow decay rate, which is the negative real part of the acoustic complex natural frequency,

   \[\begin{equation} \mathcal{J} = Re(s). \end{equation}\]

We want to find a shape for the printhead’s micro channel, which maximises the decay rate of acoustic reverberations while decreasing (or at least maintaining) the pressure drop required to flush ink through the printhead.

Amongst many different optimisation approaches we use the gradient-based one. Generating a new shape and then finding a flow solution is the most expensive part, so we need a cheap and fast way to find the shape gradients of our objective and constraints.

The most elegant way to find the sensitivities of the objectives to shape modifications is to use the adjoint approach. The adjoint approach allows us to find the objectives’ gradients with only one additional linear computation, while the direct objective evaluation is usually non-linear and very expensive. The computational cost of the adjoint method is also independent of the number of optimisation parameters, while, say, the finite-difference approach requires \(1 + N\) additional expensive objective evaluations, where \(N\) is the number of parameters to optimise.

Steady flow: direct and adjoint states

We start with the steady flow problem. We need to solve the direct problem to find flow state and the viscous dissipation. 
The direct velocity magnitude is the highest in the narrow part of the channel, which contributes the most to the viscous dissipation of the steady flow.

The viscous dissipation shape sensitivity has a known analytical expression and is proportional to both the direct and the adjoint velocity fields: \(G_\mathcal{R} = G_\mathcal{R} (\mathbf{u}, \mathbf{u}^\dagger)\). We then solve the adjoint problem, and find the adjoint velocity field. The adjoint velocity physical meaning is a sensitivity of viscous dissipation to external forcing.

The direct \(|\mathbf{u}|\) (left) and adjoint \(|\mathbf{u}^\dagger|\) (right) velocity magnitudes of the steady flow.

Oscillating flow: direct and adjoint states

The oscillating flow works a bit differently. As we are looking for a natural frequency and a natural mode of the acoustics, we solve an eigenvalue problem for the acoustic pressure, velocity and temperature. We will only target the lowest frequency natural mode, with the frequency of 350 kHz.

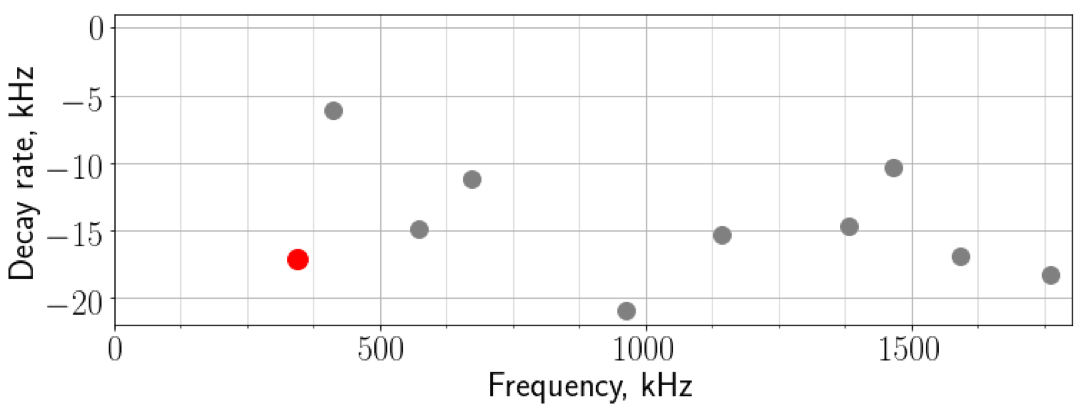
The acoustic energy mainly dissipates in the boundary layers at the nozzle and the corner regions, where the acoustic velocity amplitude is the highest.

Spatial distrubution of the acoustic energy dissipation rate (on log scale)

The beauty of the viscothermal acoustic problem is that it is self-adjoint, meaning that once the direct state is calculated, we have the adjoint fields for free and can instantly get the shape gradients. We have also derived the analical expression for the shape sensitivity of the acoustic eigenvalues, \(G_\mathcal{s} = G_\mathcal{s} (P, \mathbf{u}, T)\).

Gradient based optimization

At this point, we know how to cheaply calculate the shape gradients of the objectives: the steady flow viscous dissipation and the oscillating flow decay rate. We apply this information to some gradient-based solver. In particular, we use the method of moving asymptotes (MMA) for constrained shape optimization.

The animation shows the iterations steps and how the objective and constraint, normalised by their initial values, change during the optimization process. In 10 iterations we find a geometry with 40% larger decay rate and lower pressure drop. It means, that it only requires us 10 state evaluations and this number is independent of the number of optimisation parameters.

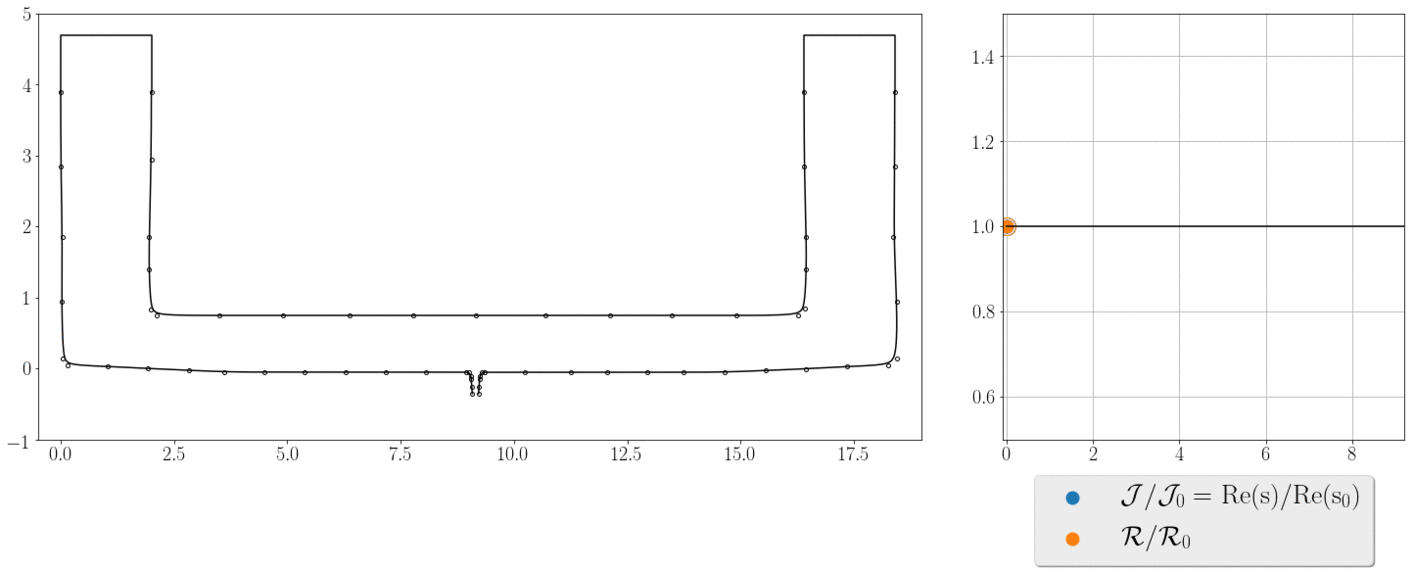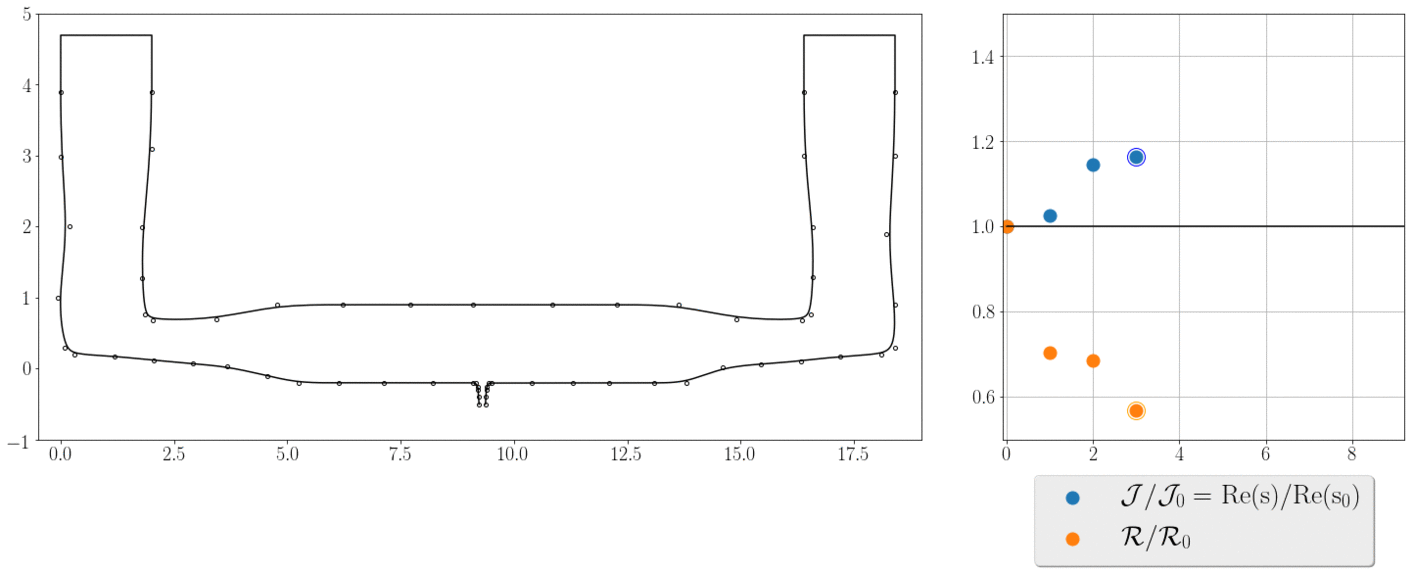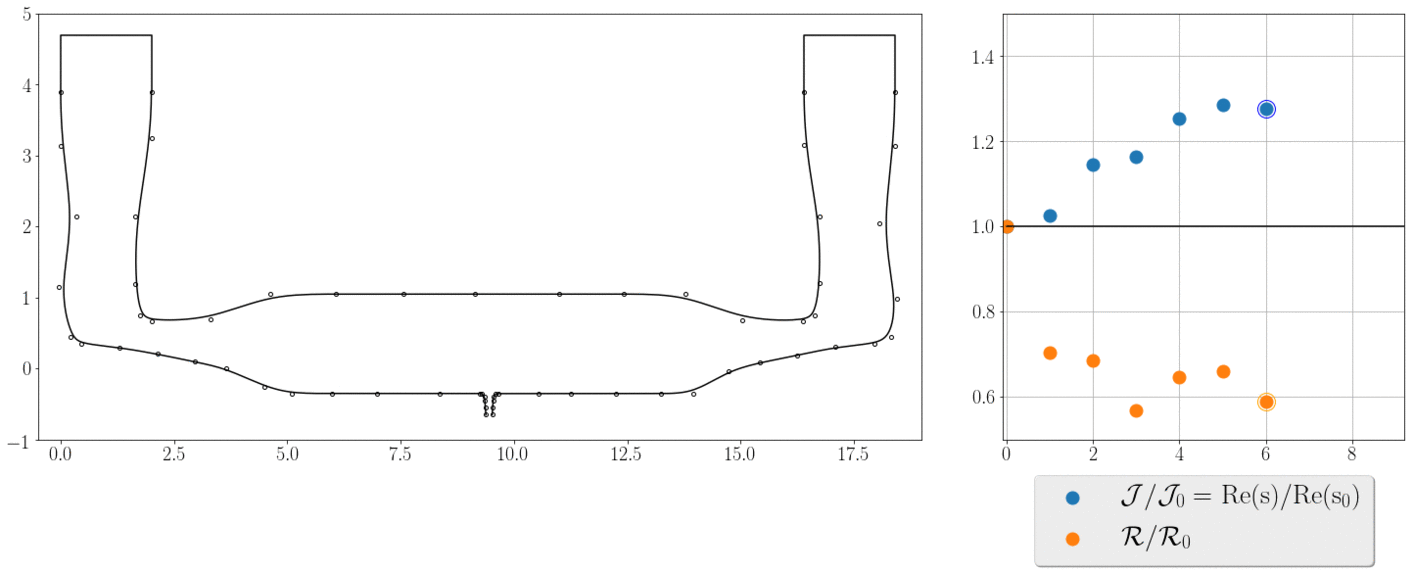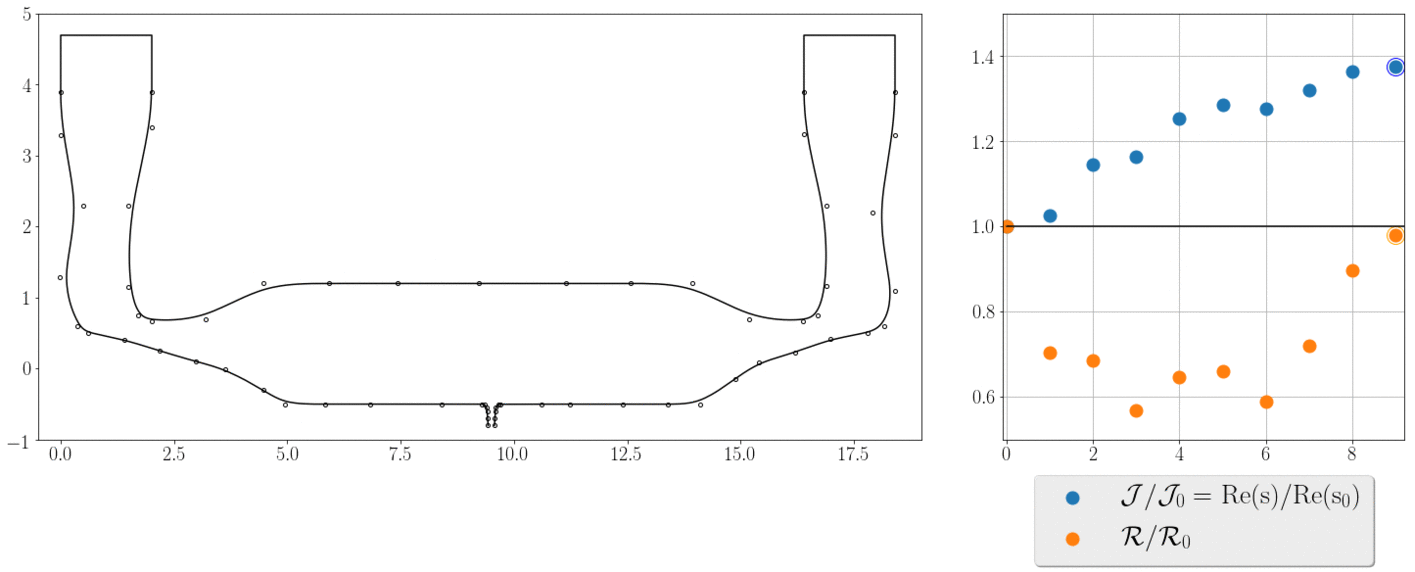
The adjoint approach is the most efficient method for gradient-based shape optimisation.

Summing up

Summing up, we split the flow inside the inkjet micro channels into the steady flow with not oscillations and the oscillating flow with no steady flow.

For two objective functions: the steady flow viscous dissipation and the oscillating flow decay rate, we have derived the shape gradients, using the adjoint method.

We then applied this gradient information to shape optimisation routine and decreased the lifetime of the residual acoustic reverberations by 40% while reducing the steady flow pressure drop. This allows us to shorten the reverberations stage and increase the printing speed.

Thanks everybody for attending and presenting at EFMC 12 in Vienna this year!